AtCoder の問題を解くために必要な実力を付けるために作られた「典型問題」を解いていく企画として、「典型90」があります。
今回は、その内、の39問目である「Tree Distance(★5)」を解説していきたいと思います。
なにか、間違っているところなどありましたら、@EitaSugiまで、ご指導ご鞭撻の程、よろしくお願い致します!
問題名 【039 – Tree Distance(★5)】
入力
N : 頂点の数
a,b : 頂点aと頂点bを双方向につなぐパス
考察
考える上で
この章は、解説ではないので読み飛ばしても大丈夫です。解説に至るまでの考えを書いてます
本問題は、各頂点(i)から、それ以外の頂点(else_i)への最短距離の総和を求める問題です
ここで私は、木の最短経路と言われているので
各頂点からの最短距離を求めるために、ダイクストラ法を用いればACできるのではないかと考えました。
しかしこれをすべての頂点について行うと
ダイクストラ法の計算量O(V((V+E)logV)//2) > O(V^2) > 10^8となりTLEとなってしまいます。
(見積もり違ったらすみませんm(_ _)m)
そのため、ダイクストラ法を用いて解くのは難しいです。そこで頂点に注目するのではなく、辺に注目します。
具体的には、すべての2点間において最短経路で移動した際にそれぞれの辺は何回使用されたかについて考えます。
本題
以下のような木構造があった場合、
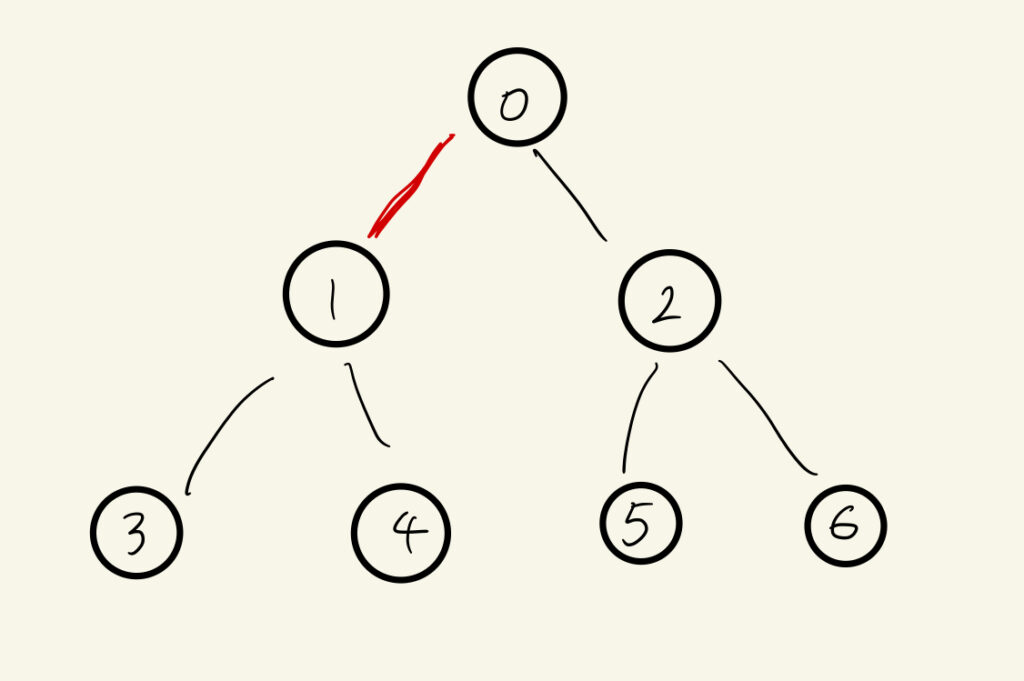
赤い辺を使用するのは、
赤い辺よりも下にある[1, 3, 4]とそれ以外の[0, 2, 5, 6]間の移動のときだけです。
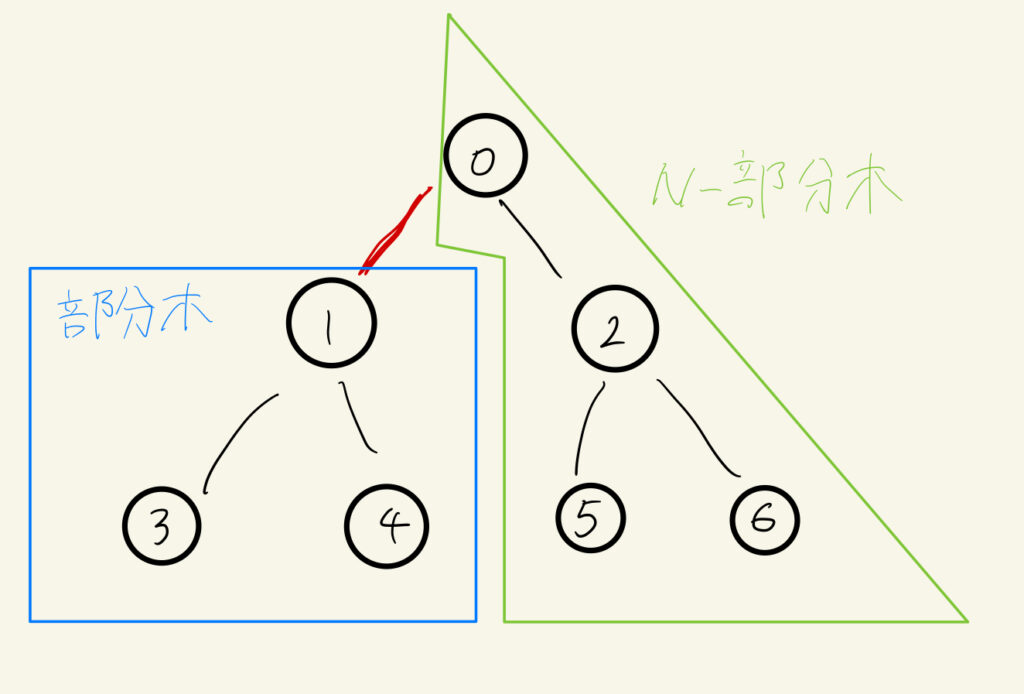
このことから、任意の辺の使用回数は
その辺よりも下にある辺の数(部分木)*それ以外(N-部分木の数)で求まります。
その辺よりも下にある辺の数(部分木)はdfs(O(V+E))で求めることができるので、dfsで求めた後、各辺の使用された回数を計算すればTLEすることなく答えにたどり着けます
コード
import sys
sys.setrecursionlimit(10 ** 7)
N = int(input())
nodes = [[] for i in range(N)]#各頂点がどの頂点とのパスを持つか格納するリスト
for i in range(N-1):
a,b = map(int, input().split())
a -= 1#0-indexにしたいので-1
b -= 1
nodes[a].append(b)#頂点aは、bへのパスを持つ
nodes[b].append(a)
A = [1 for i in range(N)]#自分のパスよりも下の部分木の個数を格納するためのリスト
flg = [True for i in range(N)]#flg
flg[0] = False
def dfs(v):
for nv in nodes[v]:#現在地vからnvへ行く
if flg[nv] == False:#既に訪れていたら
continue
else:#初めて訪れたら
flg[nv] = False#二度と訪れないようにflgを更新
dfs(nv)#nvについて部分木を探索
A[v] += A[nv]#nvまでの部分木の合計を加算
dfs(0)
ans = 0
for i in range(N):
ans += A[i] * (N-A[i])
print(ans)



コメント