Group Lassoについて解釈を深める

この記事では、僕なりのグループLassoについての解釈を説明していきます。

GroupLassoの概要

まず、grouplassoを理解する前にLasso回帰とRidge回帰について理解する必要があります。

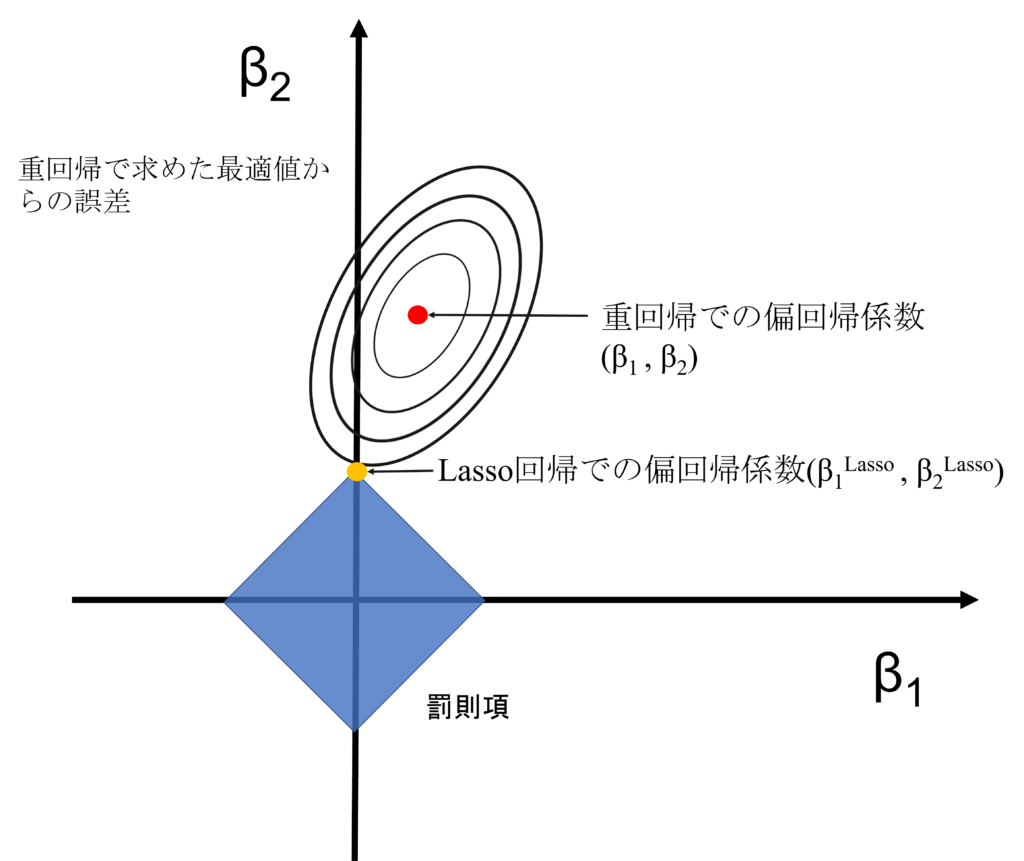
詳しい話は、別の記事で紹介しますが、簡潔に言うと、「重回帰での予測だと偏回帰係数が大きくなりすぎるから、特徴量の数を減らそう」とするのが、Lasso回帰

Lasso回帰のコスト関数

重要なのは、罰則項が絶対値によって制限されるので、罰則領域はひし形になる。

特徴量削減方法

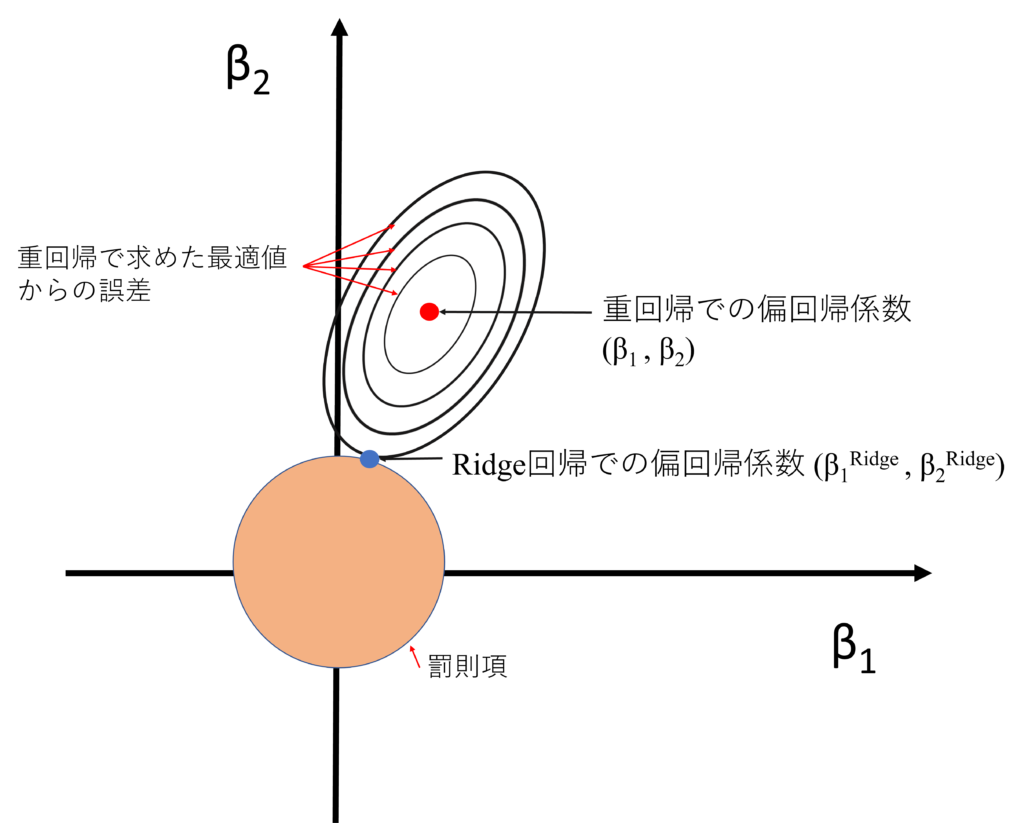
「重回帰だとトレーニングに特化しちゃうから汎化性能を上げるため、いろんな特徴量を小さくしよう」とするのが、Ridge回帰

Ridge回帰のコスト関数

重要なのは、罰則項が２乗によって制限されるので、罰則領域は円になる。

特徴量削減方法

ここから、本題であるGroupLassoの解釈について説明していきます。

GroupLassoのコスト関数は以下のように表されます。

※添字Gjは、特徴量をいくつかのGroupに分けたときの、j番目のGroupを指す

とはいえ、数式だけ見てもわからないので、具体的な手順を通して理解を深めていきましょう。

前処理
0, IV(説明変数)をいくつかのグループに分けます。

GroupLassoの処理
1, どのグループを使用するか決めます。
2, 採択されたグループ内で特徴選択を行う
3, 採択されたグループ間で特徴量選択を行う
(2,3の操作は同時に行われますが、便宜上2,3と書かせてもらいます)

ここで具体例として、
採択されたグループが[1,2]で、グループ1 = [x,y], グループ2 = [z]の場合について考えます。

今回、GroupLassoの関数は以下のとおりなので、

採択されなかったものは、係数が0になるので、今回は考える必要がなくなります。
つまり、グループ1の[x,y]とグループ2の[z]以外の係数は無視して良いです。

そのため、コスト関数のプロットは以下の通りになります。

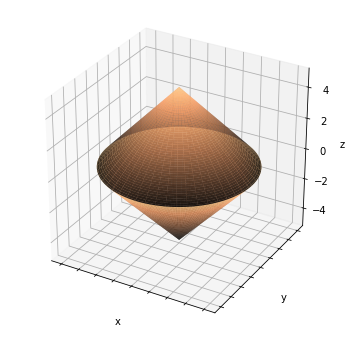
なぜなら、グループ内では、2乗和によって、特徴量が制限されますが、グループ間では正の値の加算によって、コスト関数が制限されるためです。

ここで、重要なのは、x,y平面上(グループ内)では、ridge回帰のように特徴量が選択されるのにもかかわらず、zと平面とxy超平面(グループ間)では、lasso回帰のように特徴量が選択されるということです。

僕なりの解釈では、

って感じだと思います。

以上、grouplassoの僕なりの解釈です。間違っているところあれば、連絡くださいー。
何卒宜しくお願いします。